
We have now determined the two eigenvalues and. Since the discriminant is strictly positive, this means that two different values for exist: To solve this quadratic equation in, we find the discriminant: To determine the eigenvalues for this example, we substitute in equation ( 3) by equation ( 4) and obtain: In the following sections we will determine the eigenvectors and eigenvalues of a matrix, by solving equation ( 3). Therefore, to find the eigenvectors of, we simply have to solve the following equation:
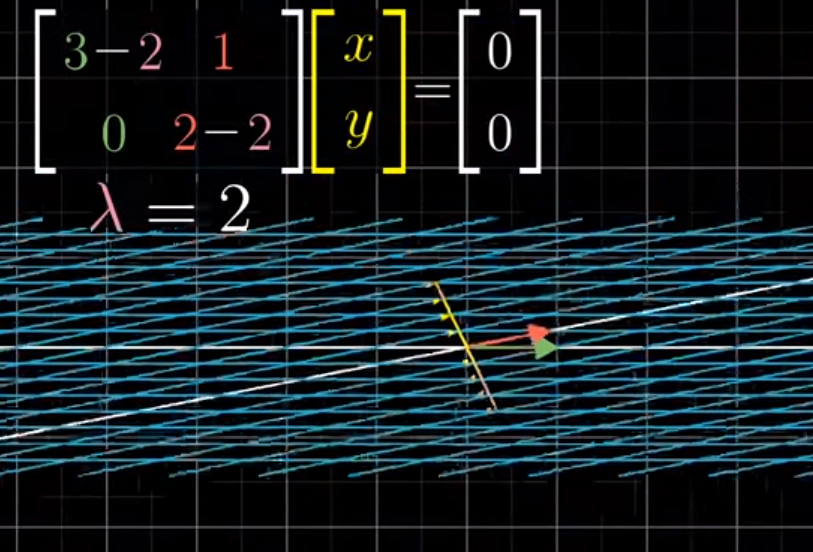
If a square matrix is not invertible, that means that its determinant must equal zero. However, assuming that is not the null-vector, equation ( 2) can only be defined if is not invertible. Where is the identity matrix of the same dimensions as. This means that the linear transformation on vector is completely defined by. Where is a scalar value called the ‘eigenvalue’. In general, the eigenvector of a matrix is the vector for which the following holds: This unique, deterministic relation is exactly the reason that those vectors are called ‘eigenvectors’ (Eigen means ‘specific’ in German). These vectors are called eigenvectors of the transformation, and uniquely define the square matrix. The above figure shows that the direction of some vectors (shown in red) is not affected by this linear transformation. The transformation in this case is a simple scaling with factor 2 in the horizontal direction and factor 0.5 in the vertical direction, such that the transformation matrix is defined as:Ī vector is then scaled by applying this transformation as. The green square is only drawn to illustrate the linear transformation that is applied to each of these three vectors.Įigenvectors (red) do not change direction when a linear transformation (e.g. Consider the image below in which three vectors are shown.
EIGEN VECTOR 2D HOW TO
In this article, I will provide a gentle introduction into this mathematical concept, and will show how to manually obtain the eigendecomposition of a 2D square matrix.Īn eigenvector is a vector whose direction remains unchanged when a linear transformation is applied to it. Furthermore, eigendecomposition forms the base of the geometric interpretation of covariance matrices, discussed in an more recent post. An interesting use of eigenvectors and eigenvalues is also illustrated in my post about error ellipses.
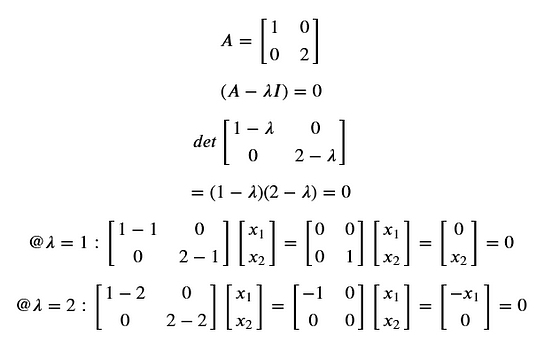
Well known examples are PCA (Principal Component Analysis) for dimensionality reduction or EigenFaces for face recognition. Eigenvectors and eigenvalues have many important applications in computer vision and machine learning in general.


 0 kommentar(er)
0 kommentar(er)
